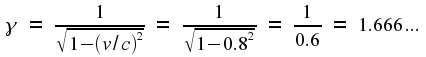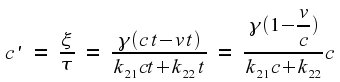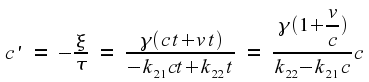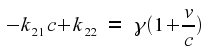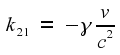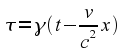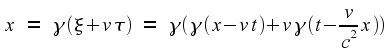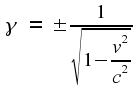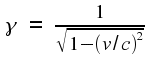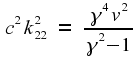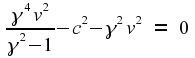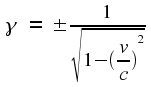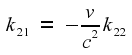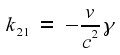Special Relativity
Introduction
Albert Einstein published his famous paper on
relativity in 1905, so it has had plenty of time to penetrate the
public consciousness. Nevertheless, it is not well understood.
Sometimes you will even hear statements to the
effect that only half a dozen people in the world understand
relativity. This is complete rubbish. The theory is routinely taught
to university students, and presumably understood by them. It is true
that the topic known as General Relativity is somewhat challenging,
and is studied only by advanced students, but that is a further
development that was not covered by Einstein's early work on
relativity. In these notes I hope to convince you that Special
Relativity, the subject of the 1905 paper, is not at all difficult to
understand. Some mathematical calculations are required, it is true,
but I hope to convince you that it is not necessary to go beyond high
school algebra.
What is relativity?
Relativity, in the sense that the word is used
here, refers to the simple idea that absolute position and speed
(with respect to the universe, for example) are not necessarily
meaningful concepts. What matters is the relative
motion between two or more objects and/or observers.
Suppose that a car
travelling at 80 km/h is rear-ended by another car travelling at 90
km/h. At what speed did the collision happen? The figures just given
are speeds relative to the road, and it might well happen that the
drivers' subsequent reactions were affected by the road-relative
speed; but, for the purpose of predicting the immediate damage
sustained by the vehicles, the important figure is 90-80=10 km/h.
That was the relative speed of the two cars. The speed relative to
the road is, at this stage, unimportant. It is also unnecessary to
take into account the effect of the earth's rotational speed, the
speed of the earth relative to the sun, the speed of the sun with
respect to the galaxy, and so on.
Of course, it is
possible that the collision could distract the driver to the extent
that the first car runs into a wall. That would indeed be an 80 km/h
collision, because that is the car's speed relative to the wall.
Again, however, the relevant speed is a relative speed.
This form of relativity
has been well understood since at least the time of Isaac Newton. In
fact, a lot of it was understood at the time of Galileo Galilei. In
that respect, Einstein added nothing new. Einstein's great
contribution was connected with the speed of light.
Light and the ether
One of my enduring childhood memories is of seeing
someone chopping wood in the distance. I was out in the country, most
likely helping my father gather firewood. In the distance, another
man was using an axe. Each time his axe hit the wood, there was no
sound. Each time he raised his axe above his head, there was a
chopping sound.
The reason for the anomaly is well known. It's
because light and sound travel at different speeds. The visual
experience depended on the speed of light. The noise of the axe
hitting the wood travelled at the speed of sound. Either the sound
must have been reaching me faster than the light, or vice versa. We
now know that light travels very much faster than sound. In fact,
this has been known for a very long time, because there have been
many experiments designed to measure the speed of sound, and many
experiments designed to measure the speed of light.
The mechanism by which sound travels is well
understood. Sound is a travelling wave made up of successive
compressions and rarefactions of air. (Or of whatever other medium
the sound is travelling through. The speed of sound through water is
very much different from its speed through air, and its speed through
a solid is different again.) The speed of sound through air can be
calculated by knowing things like the compressibility of air.
Light is also a travelling wave, but it has
nothing to do with compressions and rarefactions. Instead, it is an
oscillating magnetic field in combination with an oscillating
electric field. If you're interested, see my essay entitled
“Maxwell's Silver Hammer”.
Now, the speed of sound in air is a speed relative
to the air. If there is a wind blowing air towards the observer, the
observed speed will increase. As a first approximation, the speed of
the air will be added to the speed of the sound through the air.
That's obvious from the “relativity” concept.
What is light moving through? For a long time it
was believed that light moved through something called “the
ether”. However, the speed of light can be calculated from
Maxwell's equations, a set of equations that describe the
relationship between electrical and magnetic fields, and those
equations don't say anything about the ether. Either Maxwell's
equations need to be modified to take the ether into account, or
there isn't any ether.
The situation was clarified a little by the famous
Michelson-Morley experiment. Two experimenters named Michelson and
Morley set up an experiment designed to work out the earth's speed
relative to the ether. They discovered that the speed was zero! (Plus
or minus an experimental error, which the researchers managed to show
was very small.) Either the earth was stationary with respect to the
ether – an assumption that many people would have accepted a
few hundred years ago, but which had become disrespectable by the
19th century – or there was something wrong with the
“ether” concept.
There are several possible interpretations of the
Michelson-Morley result:
The earth is stationary, or near-stationary, with respect to the
ether. Although this is a possible conclusion, it is a bit like
assuming that the earth is the centre of the universe. We can't rule
it out, but nearly everyone has concluded that this would require a
massive and rather improbable coincidence.
Moving bodies such as the earth drag the ether along with them, so
that any large body would indeed appear to be stationary with
respect to the ether. If this were true, then the ether would be
distorted by all of the stars and planets that we can observe, which
would give distorted astronomical observations. This again is
something that is possible, but which most physicists have rejected
as implausible.
Motion with respect to the ether causes lengths to be distorted, in
such a way as to exactly cancel out the effect that Michelson and
Morley were trying to observe. This possibility did receive serious
consideration by physicists. George FitzGerald appears to have been
the first to suggest this explanation. Shortly afterwards, Hendrik
Lorentz showed that the Michelson-Morley experiment could be
explained if their apparatus was shrunk, in the direction of motion,
by a factor
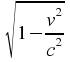 ,
where v
is the Earth's speed with respect to the ether, and c
is the speed of light. It's interesting to note that precisely this
factor turns up in the Einsteinian explanation, but for different
reasons.
,
where v
is the Earth's speed with respect to the ether, and c
is the speed of light. It's interesting to note that precisely this
factor turns up in the Einsteinian explanation, but for different
reasons.
There is no ether,
and the results have to be explained by a different theory. This is
the approach that Einstein took. Mathematically his theory is
closely similar to the theories of Lorentz, but it is based on
different reasoning.
It is not entirely clear whether Einstein was
influenced by the Michelson-Morley experiment. He had a bias towards
the “pure reason” school of thought, a bias that said
that physical laws could be deduced by reason alone, without recourse
to experimental results. Certainly other people were influenced by
the experiment sufficiently to conclude that there would be a
“contraction” effect in bodies close to the speed of
light. As it happens, however, Einstein's explanation was accepted as
the clearest description of what was observed.
Einstein's assumption was that there was no ether,
and that Maxwell's equations were valid in all inertial reference
frames. “Inertial” here means “no acceleration”.
The assumption here is that Maxwell's equations are equally valid for
observers in two frames of reference that are moving with a constant
speed with respect to each other. (Accelerations complicate the
mathematics, and that is what General Relativity is all about. The
theory of General Relativity is based, in part, on the notion that
there is no way to tell the difference between acceleration and
gravity.) Most critically, Einstein's assumption is that the speed of
light, as measured by two observers moving at constant velocity with
respect to each other, will turn out to be the same.
The speed of light
Let us consider two inertial reference frames,
moving at a speed v
in the x direction
with respect to each other. (“Inertial” simply means that
neither frame is accelerating.) The coordinates in the two frames are
(x,
y,
z,
t)
in the first frame, and (ξ,
υ,
ζ,
τ)
in the second frame. For the sake of setting up the time and
space origins, let us suppose that the origins of the two frames
coincide with each other at time t=τ=0.
From the assumed movement in the x
direction, it seems reasonable to assume that υ=y
and ζ=z.
The relationship between ξ
and x
not as obvious. From traditional mechanics, and knowing that the two
frames are moving at a constant speed with respect to each other, we
would expect the relationship to be ξ=x
–
vt.
That is, the “obvious” relationship between the two
coordinate systems is
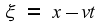
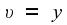
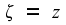
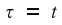
As we shall see below,
this does not work.
Suppose that a
flash of light occurs at the origin of the first frame at zero time,
and that the resulting light wavefront expands spherically at the
speed of light, which we call c.
From the viewpoint of the second frame, traditional theory would tell
us that the wavefront also expands spherically as seen in the second
frame, and that the sphere's centre moves in the -ξ
direction because of the relative motion of the two frames.
This is where
Einstein departed from tradition. The motion of a light wavefront is
governed by Maxwell's equations, and Maxwell's equations do not
depend in any way on the motion of the coordinate system. Einstein
supposed that Maxwell's equations would be equally valid in any
inertial (that is, non-accelerating) reference frame. This sounds
reasonable. The consequence, however, is that the speed of
light must be the same in every inertial reference system.
That is the point at which we break away from the traditional theory.
If that supposition is
true, then the wavefront must be expanding (at the same speed) from
the origin of both coordinate frames, since the origins were
coincident at the time the light was emitted.
The equation of an
expanding spherical surface is
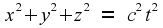
Along the x
axis, this reduces to
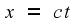
So far, so good. But if
we map this into the second frame, using the transformation that has
just been presented, the equation of the wavefront along the x
axis becomes
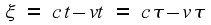
so the speed of light in the second frame is
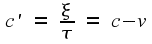
This conclusion
contradicts the idea that the speed of light should be the same in
the two frames. We are therefore forced to conclude that the
equations linking the two coordinate systems need modifying.
Modifying the coordinate transformation
The assumptions that
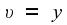 and
and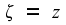 are reasonable in most people's minds. There is no motion in those
two directions, in our example, so no grounds for assuming that
motion would affect those two axes. With motion only in the x
direction, we need look only at the equations
are reasonable in most people's minds. There is no motion in those
two directions, in our example, so no grounds for assuming that
motion would affect those two axes. With motion only in the x
direction, we need look only at the equations
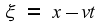
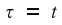
We have already seen
that those equations give contradictory conclusions about the speed
of light. Thus, we are motivated to look for modified forms of those
equations.
It is shown in the
Appendix that the transformation that works, in terms of giving the
same speed of light in both frames, is
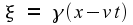

where
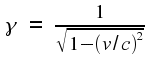
(Don't shy away from
reading the Appendix. It contains the high school algebra that I
mentioned.)
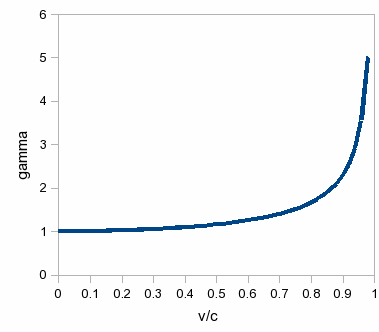 Note
that the value of γ
is always greater than one. (Or equal to one, in the special case of
zero relative speed.) For low values of v
it is very close to one, so that the transformation between frames is
essentially the same as in the non-relativistic case. It is only when
v
is a substantial fraction of c
that the relativistic effects start to become noticeable. This is
shown in the graph at right. Even at 50% of the speed of light, γ
is only a little bit bigger than 1. As we approach the speed of
light, however, γ
grows without limit.
Note
that the value of γ
is always greater than one. (Or equal to one, in the special case of
zero relative speed.) For low values of v
it is very close to one, so that the transformation between frames is
essentially the same as in the non-relativistic case. It is only when
v
is a substantial fraction of c
that the relativistic effects start to become noticeable. This is
shown in the graph at right. Even at 50% of the speed of light, γ
is only a little bit bigger than 1. As we approach the speed of
light, however, γ
grows without limit.
The Inverse Transformation
It is instructive to work out how the
transformation goes in the other direction. Starting with
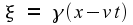

let us solve for x
and t.
The obvious first step is to write

The rest of the solution is obvious, so I won't repeat it here. The
end result is
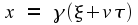

This is exactly the same as the original equations, except for the
change of sign for v.
The change of sign is because, from the point of view of frame 2,
frame 1 is moving backwards with speed v.
This is exactly what we should have expected. Indeed, it will be
obvious to anyone who has read the Appendix, because the Appendix
used these equations to work out the formula for γ.
The whole point of relativity is that there is no privileged frame.
We can think of frame 2 as moving relative to frame 1, or equally
well we can think of frame 1 as moving relative to frame 2. We should
get the same result no matter which viewpoint we take.
Length and time contractions
Think of a rigid rod that is stationary with
respect to frame 2, and oriented along the ξ
axis. Lengths are, obviously, scaled by a factor γ
between the two frames. Thus, this rod appears longer
to an observer moving with the rod than it does to an observer in
frame 1.
Equivalently, to
the observer in frame 1, seeing the rod move past with speed v,
the rod appears shorter than its length when at rest. As v
approaches the speed of light, the length of the rod appears to
shrink down to nothing.
The
same scaling factor applies to time intervals. If the observer in the
“stationary” frame 1 could observe a clock that is moving
with frame 2, the clock would appear to be running fast. Time appears
to be going faster in the “moving” frame.
A
numerical example
To
get some feel for what is happening here, let us put some numbers on
the result. Let us choose the earth for our frame 1. (The earth is
not quite an inertial reference frame, because it is following an
elliptical orbit, and therefore accelerating, around the sun. For our
present purposes, though, it is near enough to being an inertial
reference frame.) For frame 2, we choose a spaceship travelling at
80% of the speed of light, relative to the earth. The amount
of fuel needed to boost a vehicle to such a speed is beyond our
present capabilities, but for the sake of having a good example let
us assume that someone, somewhere in the future, has discovered
something better than nuclear fission.
We
must also assume that people on earth have good enough telescopes, or
other measuring instruments, so that each frame can observe the
other. (They would have to be pretty good. For such a large relative
speed, the spaceship might be out of range before anyone had worked
out where to point the telescope.) We also need a method of comparing
the clocks in the two frames. This is actually easier: all that is
needed is a radio signal that ticks once per second. Radio signals
also travel at the speed of light, so there will be a time delay, but
it is a delay that can be calculated and corrected for.
For
the given relative speed, we can calculate
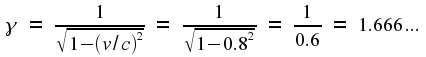
Assume,
for the sake of example, that the spaceship is 200 meters long in its
direction of travel. To an observer on Earth, it will appear to be
only 120 meters long. This is clearly a major difference.
For
the time dilation, let us suppose that the spaceship is sending out a
“clock” signal by radio that is ticking once per second.
On Earth, this will be perceived as a clock that is running 67% fast.
The Earth observer will hear 5 ticks every 3 seconds.
Think
about someone on the ship who is 20 years old when the ship is
passing the Earth. One hundred years later, Earth time, he is still
only 80 years old. All of his friends on Earth are dead – they
would have been 120 years old if they had survived – but this
person has aged by only 60 years. It sounds as if he has discovered
some approximation to the fountain of eternal youth.
Are
these contractions real?
When
I was in my first university year, a friend of my brother –
someone who was still in high school – asked me “Is there
a fourth dimension?” I was, I must admit, stumped. The possible
answers include “Yes”, “No”, “There are
many more than four dimensions”, and “It depends on what
you mean by 'dimension'”. The true answer, though, is “You
have asked the wrong question.” Once you reach the point of
knowing the answer, you also realise that the original question was
meaningless.
Relativity
is like that. The answer to most questions is “You are asking
the wrong question.” Once the question is rephrased, the answer
is “mu”.
The
previous section seemed to suggest that people on the spaceship live
longer, albeit with a weirdly distorted shape, than the people who
stayed on Earth, because their biological clocks run slower than
their clocks as measured by Earth observers. Remember, though, that
from the viewpoint of the people on the ship it is exactly the other
way around. The Earth is receding from them at 80% of the speed of
light. To them, therefore, the earth has shrunk in one direction, and
earth clocks are running slow. The situation is entirely symmetrical.
Meanwhile,
the people on the ship have no feeling that their ship has shortened,
or that their time scale is distorted. Everything feels normal to
them. The contractions do not happen from their point of view. They
are only seen by outside observers who are moving at a different
speed.
Thus,
the contractions that we see in the relativistic equations are an
observer effect. They amount to saying “If you are moving
relative to the thing you're measuring, your measurements will be
distorted”.
That
doesn't mean that there aren't practical consequences. People
travelling in a high-speed space ship will indeed notice that the
universe has been squashed. Not only that; they will get to their
destination faster (by their own clocks) than would have been
predicted by non-relativistic theories.
Appendix: Deriving the
transformation equations
As in the main text, our starting point
is one reference frame (frame 1) with coordinates (x,y,z,t),
and a second frame (frame 2), moving with speed v
in the +x
direction relative to frame 1, with coordinates (ξ,υ,ζ,τ).
The coordinate origins are chosen such that the space origins of the
two frames are coincident at the time origin
 .
.
It appears to be reasonable to start
with two assumptions:
Distances measured at right angles
to the relative motion are not affected by the motion. That is,
distances in the y
and z
directions are the same as if there had been no motion.
The relationship between the two
sets of coordinates is a linear one.
There is, perhaps, no fundamental
justification for either of these assumptions, but we have a natural
preference for looking for simple solutions before introducing
complications. If it turned out that no linear transformation worked,
then of course we would have to start looking at nonlinear
transformations; but in fact it turns out that we do get a solution
with the above assumptions, and furthermore that that solution agrees
with what is found by experiment.
With these assumptions, we are looking
for a transformation of the form



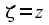
where the kij
are constants whose values have to be discovered. The last two
equations say that we can ignore what is happening in the y
and z
directions, reducing the problem down to
one space dimension and one time dimension.
One
thing that should be immediately obvious is that the origin of frame
2, the point
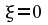 ,
coincides with the moving point
,
coincides with the moving point
 in frame 1. That, after all, is simply a restatement of the fact that
frame 2 is moving with speed v in the +x direction, relative to frame
1. This means that
in frame 1. That, after all, is simply a restatement of the fact that
frame 2 is moving with speed v in the +x direction, relative to frame
1. This means that
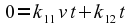
from
which it follows that
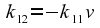 .
In the main text we will use the symbol
.
In the main text we will use the symbol
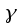 to mean
to mean
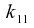 ,
so let us make that change of notation right now. This leaves us with
the transformation equations
,
so let us make that change of notation right now. This leaves us with
the transformation equations
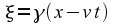

We are
now down to three constants whose value we have to find.
A flash of light in the x
direction
A typical
treatment of this subject considers what will happen when a flash of
light occurs at the time that the two origins coincide, and then
expands spherically in both frames. The basic assumption is that the
wavefront must expand at the same speed, regardless of whether we're
measuring it from frame 1 or from frame 2. Although that approach
does lead to a solution, it's simpler to reduce the problem down to
one spatial dimension, looking only at
how the light travels along the x
axis.
Consider a case
where light is emitted in the +x
direction at the
time the two origins coincide. In the first frame, the wavefront on
the x
axis is described
by
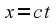 .
In the second frame, this maps to
.
In the second frame, this maps to
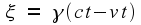
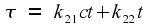
Thus the speed of the
wavefront, as measured in the second frame, is
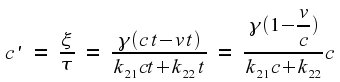
To make this exactly
equal to c,
we need

Now, let us
repeat the experiment, this time with the light being emitted in the
-x
direction at the
time the two origins coincide. In the first frame, the wavefront on
the x
axis is described by
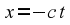 .
In the second frame, this maps to
.
In the second frame, this maps to

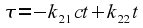
Thus the speed of the
wavefront, as measured in the second frame, and allowing for the fact
that it is moving backwards, is
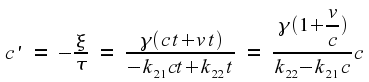
To make this exactly
equal to c,
we need
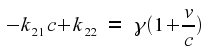
For light in the
forward direction, we found the constraint

Adding these two
equations, we get

and therefore, of
course,
 .
This allows us to solve for
.
This allows us to solve for
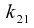 .
The end result is
.
The end result is

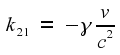
This means that the
coordinate transformation has the form
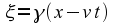
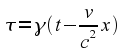
and the only remaining
thing to be found is the value of γ.
Shifting our focus to the other reference
frame
So far we have taken
the viewpoint that frame 2 is moving relative to frame 1. It makes
equal sense to treat frame 2 as the “stationary” frame,
with frame 1 moving backwards relative to it. (Of course,
“stationary” is a label of convenience here. In
relativity theories, every inertial frame is an equally good
reference frame.) From this viewpoint, the frame 1 coordinates must
be able to be expressed in terms of the frame 2 coordinates using the
transformation that we have already established. That is,
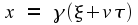

The
essential point here is that these are the same equations as were
used for the original transformation. The v
terms have changed sign, because the relative motion is now in the
opposite direction, but otherwise we have the same equations, with
the same γ. This is
an important point. If all inertial frames are equally good reference
points, then the transformation equations should be the same between
any pair of inertial frames.
Of
course, this will not work for just any arbitrary γ.
You would be right in guessing that γ
has to be restricted in order
to give consistent results. Let us now explore this point.
Expanding
out the first equation, we get
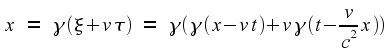
which reduces down to

Clearly, this can work only if
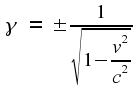
Technically, this gives two different
solutions for γ.
If you look at the transformation equations, though, you will see
that the negative solution is no different from the positive solution
apart from what is, in effect, a relabelling of the axes to make one
of them point in the opposite direction. This is a difference that
changes nothing important, so we are justified in deciding to use
only the positive solution. Our conclusion, then, is that
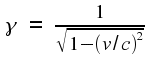
Note that this formula has no meaning
in real arithmetic if
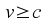 .
We could play some interesting games with the equations if we decide
to allow complex arithmetic, but there are reasons for believing that
nothing can be accelerated beyond the speed of light, relative to
whichever reference frame you want to use. The reasons for this go
beyond the scope of this article, but broadly speaking the reason is
that infinite energy would be required. In this article we are
looking only at how distance and time measurements are affected by
relative motion, but the theory can be extended by looking at how
Special Relativity affects the notions of momentum and energy. It
turns out that the energy needed to accelerate an object also depends
on γ,
and γ
grows without bound as we approach the speed of light.
.
We could play some interesting games with the equations if we decide
to allow complex arithmetic, but there are reasons for believing that
nothing can be accelerated beyond the speed of light, relative to
whichever reference frame you want to use. The reasons for this go
beyond the scope of this article, but broadly speaking the reason is
that infinite energy would be required. In this article we are
looking only at how distance and time measurements are affected by
relative motion, but the theory can be extended by looking at how
Special Relativity affects the notions of momentum and energy. It
turns out that the energy needed to accelerate an object also depends
on γ,
and γ
grows without bound as we approach the speed of light.
There are, it is true, some theories
that deal with tachyons, which are hypothetical particles that travel
with a speed greater than light speed. It is not yet known whether
tachyons exist, but if they do exist they would not contradict the
previous paragraph. They don't need to be accelerated beyond the
speed of light because their initial speed never was below the speed
of light. Indeed, if tachyons exist then it would require infinite
energy to decelerate them to the speed of light. The speed-of-light
barrier is a barrier in both directions.
A flash of light expanding spherically
This section is
redundant, because we have already worked out the required
transformation in the preceding sections. It is included only in case
you would prefer to see a different derivation. You can skip it if
you wish. I present this alternative derivation with some reluctance,
because the mathematics is more complicated in this case; but it
seems to be the derivation preferred by textbooks.
Consider the same
setup, except that the light has no preferred direction, but expands
spherically in all directions. At any instant of time, the wavefront
of the light is the surface of a sphere centred on the origin. In
frame 1, this sphere is described by the equation
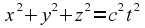
In frame 2 the wavefront is also the surface of a sphere centred at
the origin, described by the equation

which can be rewritten
as

We can eliminate y and
z by subtracting the frame 1 equation, to give
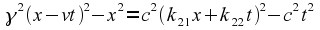
Expanding this out, and
combining like terms, we get
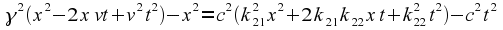
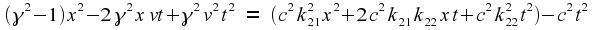
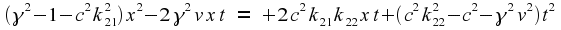

What does this
mean? If we were talking about light moving only in the x
direction, we could substitute
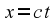 to get a result that would turn out not to be interesting. In this
case, however, we are looking at a three-dimensional expanding
sphere, so that the above should hold for any y
and z
on the sphere, even though y
and z
do not appear in the equation. This means, in effect, that we can
treat x
and t
as if they were independent variables.
to get a result that would turn out not to be interesting. In this
case, however, we are looking at a three-dimensional expanding
sphere, so that the above should hold for any y
and z
on the sphere, even though y
and z
do not appear in the equation. This means, in effect, that we can
treat x
and t
as if they were independent variables.
In that case, though,
the only way the equation can hold is if all coefficients are zero.
We are therefore forced to conclude that
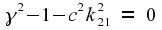

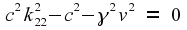
The second of these
equations can be written as

If we substitute this
in the first equation, we get

or
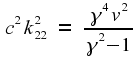
Putting this into the
third of our original equations, we get
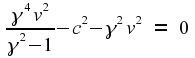
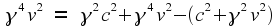
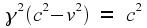
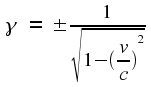
(Notice that there are
two solutions. We will return to this point later.) Now that we have
the solutions for one of the unknowns, the other two follow easily.
The results are
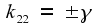
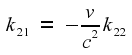
Because of the signs,
we now have four solutions. Multiple solutions are normal if you
start with quadratic equations, but it is possible for some solutions
to be spurious, i.e. not true solutions but merely pseudo-solutions
introduced because squaring a term eliminated a minus sign. In fact,
two of those solutions are spurious. Recall from the previous section
that we must have

Substituting
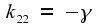 into this equation leads to a contradiction, so we are left with only
the case where
into this equation leads to a contradiction, so we are left with only
the case where
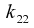 and
and
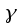 have the same sign. That cuts the possibilities down to only two
solutions:
have the same sign. That cuts the possibilities down to only two
solutions:
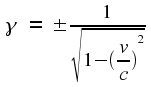

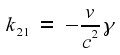
Of these, only the case
where is positive is interesting. The other case amounts to a simple
relabelling of the frame 2 axes, i.e. it is not really a separate
solution.
Finally, then, the
coordinate transformation is
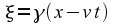
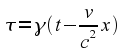
where

This article by Peter
Moylan
Other articles
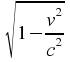 ,
where v
is the Earth's speed with respect to the ether, and c
is the speed of light. It's interesting to note that precisely this
factor turns up in the Einsteinian explanation, but for different
reasons.
,
where v
is the Earth's speed with respect to the ether, and c
is the speed of light. It's interesting to note that precisely this
factor turns up in the Einsteinian explanation, but for different
reasons.
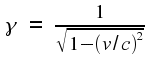
 Note
that the value of γ
is always greater than one. (Or equal to one, in the special case of
zero relative speed.) For low values of
Note
that the value of γ
is always greater than one. (Or equal to one, in the special case of
zero relative speed.) For low values of